Hey guys,
Long weekend (fallout 3 came out, had an intense test in one of my classes, work, etc).
I've got a group project coming up. Our topic is on electric cars, and we need to write a huge paper, make a 30 min presentation (among other things).
Any electric car gurus out there want to point me to some sites full of info? I'd appreciate it!
Sometimes chatting about what I've been learning at University helps it sink in more. Here's some ramblings about electricity and electrical devices. Feel free to leave a comment if you want to talk about a particular subject.
Wednesday, October 27, 2010
Saturday, October 23, 2010
Matlab and Linear Discrete Signals
Hey guys,
Today I want to talk about a program I use in my Linear Signals and Systems course. It's called MATLAB, created by MathWorks. I use it for discrete signal plotting as well as tough math problems.
You can create some nice graphs with it as well as code up some interesting scenarios for systems. Make Differential Equations a little bit easier! Any of you guys use a similar program to MATLAB? I'd like to know some alternatives if they're out there.
Today I want to talk about a program I use in my Linear Signals and Systems course. It's called MATLAB, created by MathWorks. I use it for discrete signal plotting as well as tough math problems.
Taken from the MathWorks website, this shows some of the things MATLAB can do.
You can create some nice graphs with it as well as code up some interesting scenarios for systems. Make Differential Equations a little bit easier! Any of you guys use a similar program to MATLAB? I'd like to know some alternatives if they're out there.
Friday, October 22, 2010
Electronic Breadboards
Hey guys,
In lab I use these things all the time. They're a really cool way to make a circuit without soldering, and reusable over and over again. I found it neat how they're designed by watching this video:
http://www.youtube.com/watch?v=oiqNaSPTI7w
In lab I use these things all the time. They're a really cool way to make a circuit without soldering, and reusable over and over again. I found it neat how they're designed by watching this video:
http://www.youtube.com/watch?v=oiqNaSPTI7w
Thursday, October 21, 2010
This day in Electrical History
On October 21, 1879 Thomas Edison created a light bulb that lasted 13.5 hours.
Without this invention, we'd still be lighting candles and lamps every night (and putting up with all that smoke). The only downside is now it's harder to see the stars in the sky from all the light cities put out!
Here's a picture of the earth at night taken by NASA. Check out those big cities! Shame about the places with no lights yet.
Without this invention, we'd still be lighting candles and lamps every night (and putting up with all that smoke). The only downside is now it's harder to see the stars in the sky from all the light cities put out!
Here's a picture of the earth at night taken by NASA. Check out those big cities! Shame about the places with no lights yet.
Wednesday, October 20, 2010
Midterm tomorrow
Huge test tomorrow for one of my Minor's classes (computer engineering minor, hate it. programming sucks).
Hopefully I'll survive the day, lol. Wish me some luck, brothers.
Hopefully I'll survive the day, lol. Wish me some luck, brothers.
Tuesday, October 19, 2010
DC vs AC Power
DC power, or Direct Current power was the first power to fully electrify a city (Brockton, Massachusetts). Thomas Edison designed it that way, and invested heavily in DC power plant technology. He ran into some problems, however.
Edison wanted to keep the voltage low(100V), to keep people safe. The loss of voltage at these low levels due to the transmission wire's resistance was significant. (Vload=Vsource-IRwire) He sought out some solutions, but they had problems as well. He could reduce the wire resistance by increasing the wire's cross section, but that would really impact the cost of the wires. He could have a large amount of wires transmitting to high demand areas, but again, the cost would soar. In electricity distribution, money is what matters, and Edison was a businessman.
The solution to Edison's problems came from Nikola Tesla,a Croatian scientist Edison brought the the United States to help him. Tesla suggested using AC power, or Alternating Current power. He suggested this because of an invention known as a transformer only works in AC power, and it could jack up the voltage across the wires reducing lost voltage. Then when it got to the load, it could be stepped back down to safe levels by another transformer. It solved all the problems and was cheaper than DC's solutions to the voltage problem.
Edison hated the idea of AC because he had so much invested in DC. He argued that the high voltage transmission lines were far too dangerous, and went to great lengths to get the public on his side (even publicly electrocuting animals, such as elephants). Eventually he was converted, and the AC we use today proliferated.
A lot of our devices we use today run off DC sources (a nintendo DS, for example, gets charged off DC. the plug has a AC/DC converter to change the outlet to DC and a lower voltage. I've even designed an AC/DC converter in a lab before, so it's not that complicated.
Edison wanted to keep the voltage low(100V), to keep people safe. The loss of voltage at these low levels due to the transmission wire's resistance was significant. (Vload=Vsource-IRwire) He sought out some solutions, but they had problems as well. He could reduce the wire resistance by increasing the wire's cross section, but that would really impact the cost of the wires. He could have a large amount of wires transmitting to high demand areas, but again, the cost would soar. In electricity distribution, money is what matters, and Edison was a businessman.
The solution to Edison's problems came from Nikola Tesla,a Croatian scientist Edison brought the the United States to help him. Tesla suggested using AC power, or Alternating Current power. He suggested this because of an invention known as a transformer only works in AC power, and it could jack up the voltage across the wires reducing lost voltage. Then when it got to the load, it could be stepped back down to safe levels by another transformer. It solved all the problems and was cheaper than DC's solutions to the voltage problem.
An example of an AC signal
Edison hated the idea of AC because he had so much invested in DC. He argued that the high voltage transmission lines were far too dangerous, and went to great lengths to get the public on his side (even publicly electrocuting animals, such as elephants). Eventually he was converted, and the AC we use today proliferated.
A lot of our devices we use today run off DC sources (a nintendo DS, for example, gets charged off DC. the plug has a AC/DC converter to change the outlet to DC and a lower voltage. I've even designed an AC/DC converter in a lab before, so it's not that complicated.
Monday, October 18, 2010
Electronic Configuration of Silicon
Ah, the good Ol' Periodic Table of the Elements. Thought finishing Chemistry class would be the end of this bad boy? No way. It's a useful tool for many, many professions.
The electronic configuration of an atom lists how many electrons are in each of its electron orbits. The outer shells are particularly important to an electrical engineer.
Let's look at Hydrogen, or H on the chart. It's electron configuration would be 1s^1, for having one electron in its outer shell (also it's only shell). Helium would then be 1s^2, filling up that first orbit. Those elements with full orbits are often called Noble Gases because they're highly stable (they don't crave any electrons because their outer shell is full, so they're less likely to bond with other elements spontaneously).
Moving on to Lithium, we have 1s^2 2s^1, meaning it's first orbit is full, and its second orbit has one electron. Other elements can be written in shorthand (because we often just care about the free electrons in the outer shell) using the noble gas preceding the element on the periodic table. This shorthand looks like this:
[He] 2sd^1
A nice chart labeling all the different letters for different orbits:
So, Silicon would be 1s^2 2s^2 2p^6 3s^2 3p^2
or simply [Ne] 3s^2 3p^2
These places have some great charts or lists for quick look-ups:
http://www.chemicalelements.com/show/electronconfig.html
http://www.science.co.il/ptelements.asp
Sunday, October 17, 2010
200 GHz processers?
Tektronix, Inc plans on taking some IBM chips well beyond 30 GHz. They're aiming for 200!
The new technology is expected to come out soon, or so they say.
http://www2.tek.com/cmswpt/prdetails.lotr?ct=PR&cs=News+Release&ci=17452&lc=EN
The new technology is expected to come out soon, or so they say.
http://www2.tek.com/cmswpt/prdetails.lotr?ct=PR&cs=News+Release&ci=17452&lc=EN
Saturday, October 16, 2010
Bush Gardens
Hey guys,
I went to the Bush Gardens amusement park nearby today. Just got back, so no neat post for today, obviously. Sorry about that.
I planning a few things for tomorrow's, and I think I've got something together. Lot's of homework coming up next week as well, so plenty of material I need to contemplate. See you 'round!
I went to the Bush Gardens amusement park nearby today. Just got back, so no neat post for today, obviously. Sorry about that.
I planning a few things for tomorrow's, and I think I've got something together. Lot's of homework coming up next week as well, so plenty of material I need to contemplate. See you 'round!
Friday, October 15, 2010
Physical constants
Hey guys,
In order to get the A's that the girl in my class is getting, I have to memorize some stuff. Here's some of the physical constants I'll be using in my equations. Time to type some stuff up in excel!
I might do some derivations for the equations I have to memorize later today. Either that, or I'll post the properties of intrinsic Silicon and intrinsic Gallium Arsenide I have to memorize. Thanks for sticking around, and ask any questions you might have about any posts.
In order to get the A's that the girl in my class is getting, I have to memorize some stuff. Here's some of the physical constants I'll be using in my equations. Time to type some stuff up in excel!
| Physical Constants | ||
| Angstrom | Å | 0.1 nm |
| Avagadro constant | Nav | 6.022x10^23 |
| Boltzmann constant | k | 1.38066x10^-23 J/K |
| Elementary charge | q | 1.602x10^-19 C |
| Electron rest mass | m0 | 9.1094x10^-31 kg |
| Electron Volt | eV | 1.602x10^-19 J |
| Gas constant | R | 1.98719 cal/mol*K |
| Permeability in vacuum | μ0 | 1.25664x10^-8 H/cm |
| Permittivity in vacuum | ε0 | 8.85418x10^-12 F/cm |
| Planck's constant | h | 6.62607x10^-34 J*s |
| Reduced Planck's constant | ℏ | 1.05457x10^-34 J*s (or h/2π) |
| Speed of light in a vacuum | c | 2.99792x10^10 cm/s |
| Thermal voltage at 300K | kT/q | 0.025852 V |
| Wavelength of 1 eV quantum | λ | 1.23984μm |
I might do some derivations for the equations I have to memorize later today. Either that, or I'll post the properties of intrinsic Silicon and intrinsic Gallium Arsenide I have to memorize. Thanks for sticking around, and ask any questions you might have about any posts.
Thursday, October 14, 2010
Failed Tests and The Hall Effect
Ok guys,
Just got back my Semiconductor materials test, very low grade (like most of the class, actually). :(
Talked with some of the students from last year, and they said it was a similar situation then. The tests this teacher give out are monsterously difficult, nothing like the homework or examples, and hardly any information is given about each problem. One person scored 100, and she actually memorized dozens of physical constants as well as nearly all the parameters of intrinsic Silicon and intrinsic Gallium Arsenide semiconductors at 300 kelvin...so yeah. She did a great job (and she's rather cute, too). We'll have to put in as many hours as she does if we're going to pass this class. I'm still upset the teacher refused to give us most of the physical constants and none of the equations we needed, but it really made me think during the test.
My burning academic career aside, let's talk about the Hall Effect. Here's a nifty picture taken from my professor's lecture (forgive my larcenous ways!)
Let's say we have a chunk of semiconductor material that's p-type (doped so that the carrier concentration favors holes left by absent electrons).
Let's say we jam some wires on the left and right side and run a voltage through that thing positive side on the left, negative on the right. What will happen? The voltage will push the holes through the semiconductor torwards the right (x-axis).
Now let's say we get an electromagnet and place a pole on the long, close side and another pole on the far side(z-axis). Now what happens? The Hall Effect.
A magnetic field perpendicular to the hole's path forms on the z-axis, inducing an electric field downwards through the semiconductor material. This electric field applies an upwards force on the hole. Like in the picture, the hole curves up under the effect of two forces (one right, one up). This leads to a collection of negative charge on the bottom of the material, and a collection of positive charge on the top of the material.
Now if you were to break out a meter and read the top and bottom of the material, you'd get a voltage reading! Magnet off, nothing. Magnet back on, Voltage!
Just by applying a voltage on either end and a magnetic field, a new voltage can be created. This new voltage can even help you calculate how many atoms of 'doping' material are in the semiconductor, a difficult feat if you don't know it and it isn't labeled.
There are several pages of equations (I have to memorize like everything else -_-) and derivations to actually prove all this. I could touch on it later if anyone wants me to go through that torture.
Later guys
Just got back my Semiconductor materials test, very low grade (like most of the class, actually). :(
Talked with some of the students from last year, and they said it was a similar situation then. The tests this teacher give out are monsterously difficult, nothing like the homework or examples, and hardly any information is given about each problem. One person scored 100, and she actually memorized dozens of physical constants as well as nearly all the parameters of intrinsic Silicon and intrinsic Gallium Arsenide semiconductors at 300 kelvin...so yeah. She did a great job (and she's rather cute, too). We'll have to put in as many hours as she does if we're going to pass this class. I'm still upset the teacher refused to give us most of the physical constants and none of the equations we needed, but it really made me think during the test.
My burning academic career aside, let's talk about the Hall Effect. Here's a nifty picture taken from my professor's lecture (forgive my larcenous ways!)
Let's say we have a chunk of semiconductor material that's p-type (doped so that the carrier concentration favors holes left by absent electrons).
Let's say we jam some wires on the left and right side and run a voltage through that thing positive side on the left, negative on the right. What will happen? The voltage will push the holes through the semiconductor torwards the right (x-axis).
Now let's say we get an electromagnet and place a pole on the long, close side and another pole on the far side(z-axis). Now what happens? The Hall Effect.
A magnetic field perpendicular to the hole's path forms on the z-axis, inducing an electric field downwards through the semiconductor material. This electric field applies an upwards force on the hole. Like in the picture, the hole curves up under the effect of two forces (one right, one up). This leads to a collection of negative charge on the bottom of the material, and a collection of positive charge on the top of the material.
Now if you were to break out a meter and read the top and bottom of the material, you'd get a voltage reading! Magnet off, nothing. Magnet back on, Voltage!
Just by applying a voltage on either end and a magnetic field, a new voltage can be created. This new voltage can even help you calculate how many atoms of 'doping' material are in the semiconductor, a difficult feat if you don't know it and it isn't labeled.
There are several pages of equations (I have to memorize like everything else -_-) and derivations to actually prove all this. I could touch on it later if anyone wants me to go through that torture.
Later guys
Today's Post
Today's post is going to be later in the day than usual. I'm in class all day, so I don't think I'll get around to it until later. See you then, guys!
Wednesday, October 13, 2010
Power's relationship with Ohm's Law
Hey guys,
Today we're going to quickly review power's relationship with Ohm's Law (what we covered last time, V=I*R). Power is what your energy company charges you for, so you might want to pay attention!
We'll add on P = I * V
Where P = Watts (w) of power. One watt is equal to one Joule of energy expended in one second.
Well, what if we only have Voltage and Resistance? What if we only have Current and resistance? How can we solve for the power in a circuit? Ohm's Law (you'll see Ohm's Law a lot)
Since we have V = I*R, then we also have I = V/R (from dividing both sides by R)
Now substitute IR for V, or V/R for I (depending on what we're given to solve for P, and we have two more equations for power:
P = (V^2)/R
P = (I^2)*R
Now it's easy to solve for P if you're only given two of the variables in a circuit.
A great picture can be found at the12volt.com that neatly illustrates the relationship between power, voltage, current, and resistance. Check it out.
http://www.the12volt.com/ohm/ohmslaw.asp
Today we're going to quickly review power's relationship with Ohm's Law (what we covered last time, V=I*R). Power is what your energy company charges you for, so you might want to pay attention!
We'll add on P = I * V
Where P = Watts (w) of power. One watt is equal to one Joule of energy expended in one second.
Well, what if we only have Voltage and Resistance? What if we only have Current and resistance? How can we solve for the power in a circuit? Ohm's Law (you'll see Ohm's Law a lot)
Since we have V = I*R, then we also have I = V/R (from dividing both sides by R)
Now substitute IR for V, or V/R for I (depending on what we're given to solve for P, and we have two more equations for power:
P = (V^2)/R
P = (I^2)*R
Now it's easy to solve for P if you're only given two of the variables in a circuit.
A great picture can be found at the12volt.com that neatly illustrates the relationship between power, voltage, current, and resistance. Check it out.
http://www.the12volt.com/ohm/ohmslaw.asp
Tuesday, October 12, 2010
Understanding Ohm's Law (and other equations)
Ohm's Law, I believe, is the most used equation in electronics analysis. It is the fundamental building block for knowing what's going on in any particular circuit.
V = I * R
Where:
V is the potential in Volts (V)
I is the current flow in Amperes (A)
R is the resistance in Ohms (Ω)
So, one Volt of potential is equal to one Ampere of current multiplied by one Ohm of resistance. Using this equation, if you have two know variables you can easily solve for the third.
Let me explain what these variables mean.
Voltage (V)
Voltage is the electric potential of a circuit. Electricity flows like water. If you have two bodies of water, one higher than the other and both connected with a sloping pipe, water would flow from the higher potential body of water to the lower potential body of water. In the diagram below, the water from Tank A should flow towards Tank B because of the potential difference they have.
Current (A)
The electric current in a circuit is the flow of electrons through it. A single electron has a charge of roughly 1.602 x 10 ^-19 Coulombs. One Ampere is equal to one Coulomb divided by one Second.
This is the flow of charge per second. An example would be to measure the amount of water leaving Tank A above and flowing into Tank B per second. That would be the current of water flowing.
Resistance (Ω)
The resistance of a circuit is a measurement of how hard it resists the flow of charge. In our water example above, there are two examples of resistance. One is the friction from the pipe slowing the water down, and the other is the size of the pipe itself. If the pipe is too small, only a limited amount of water can flow through. In a circuit, the resistivity of the materials is like the friction inside the pipe. The length of the wires connecting the devices is kind of like the width of the pipe.
So we have Ohm's Law at
The electrical potential of a circuit is equal to the flow of charge each second multiplied by the resistance to that charge. A concept to be thought about, rather than a bunch of letters.
With all the equations being thrust upon you at school, it's not hard to see them as just letters and numbers to be memorized and later forgotten. If you look at a formula and break it down into its units, and try to voice out what the formula implies, you can really grasp what's going on and learn a lot.
V = I * R
Where:
V is the potential in Volts (V)
I is the current flow in Amperes (A)
R is the resistance in Ohms (Ω)
So, one Volt of potential is equal to one Ampere of current multiplied by one Ohm of resistance. Using this equation, if you have two know variables you can easily solve for the third.
Let me explain what these variables mean.
Voltage (V)
Voltage is the electric potential of a circuit. Electricity flows like water. If you have two bodies of water, one higher than the other and both connected with a sloping pipe, water would flow from the higher potential body of water to the lower potential body of water. In the diagram below, the water from Tank A should flow towards Tank B because of the potential difference they have.
Current (A)
The electric current in a circuit is the flow of electrons through it. A single electron has a charge of roughly 1.602 x 10 ^-19 Coulombs. One Ampere is equal to one Coulomb divided by one Second.
This is the flow of charge per second. An example would be to measure the amount of water leaving Tank A above and flowing into Tank B per second. That would be the current of water flowing.
Resistance (Ω)
The resistance of a circuit is a measurement of how hard it resists the flow of charge. In our water example above, there are two examples of resistance. One is the friction from the pipe slowing the water down, and the other is the size of the pipe itself. If the pipe is too small, only a limited amount of water can flow through. In a circuit, the resistivity of the materials is like the friction inside the pipe. The length of the wires connecting the devices is kind of like the width of the pipe.
So we have Ohm's Law at
The electrical potential of a circuit is equal to the flow of charge each second multiplied by the resistance to that charge. A concept to be thought about, rather than a bunch of letters.
With all the equations being thrust upon you at school, it's not hard to see them as just letters and numbers to be memorized and later forgotten. If you look at a formula and break it down into its units, and try to voice out what the formula implies, you can really grasp what's going on and learn a lot.
Monday, October 11, 2010
Crystal Lattices and Nobel Prizes
Hey guys,
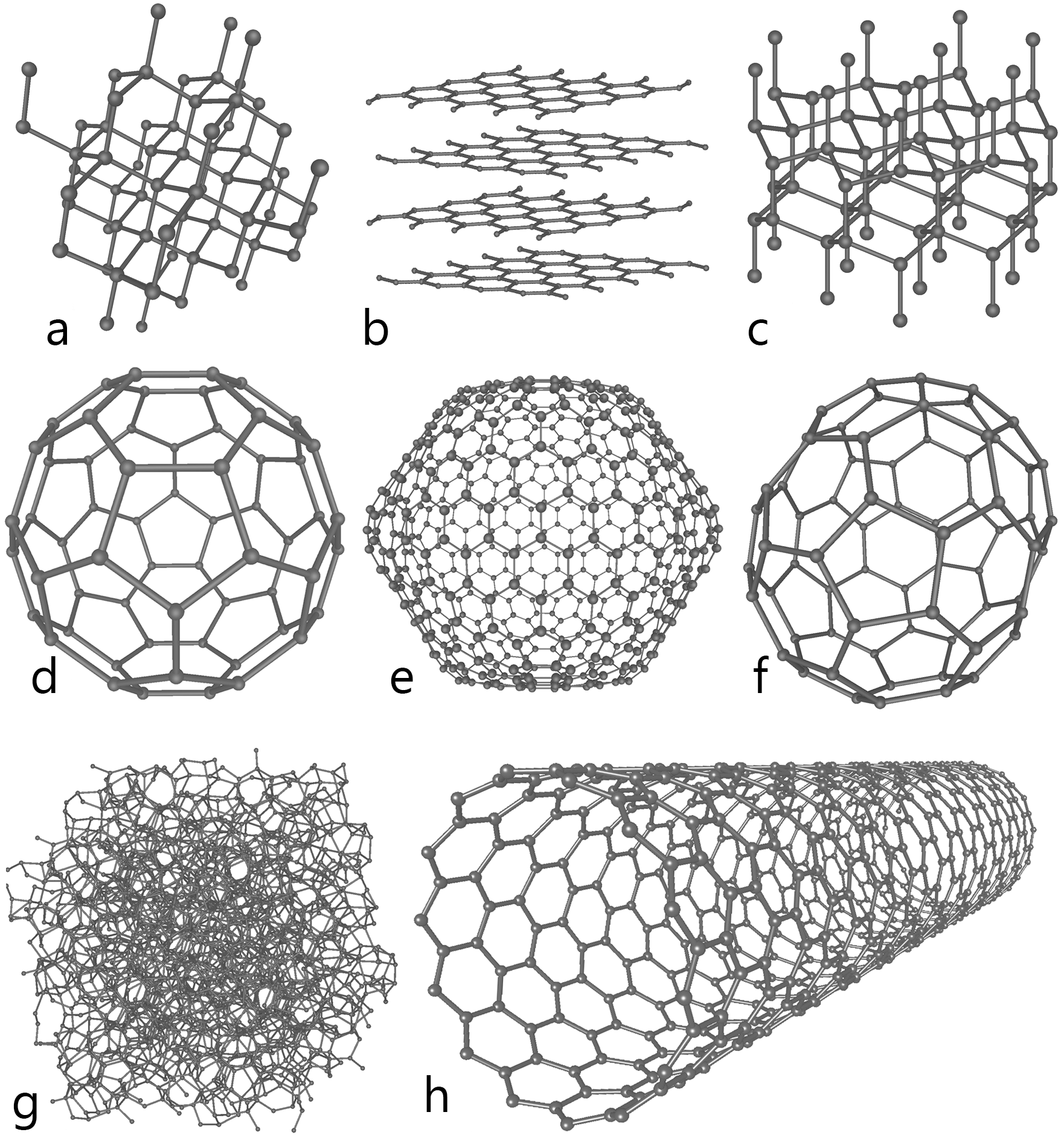
Today's topic is on graphene and it's crystal lattice. Semiconductors are "grown" in these lattices using expensive equipment.
Carbon, in particular, grows in many different forms, from diamonds to pencil lead (yes, you can even make diamonds in a lab). Graphite is used in pencil lead because its layers detaches from the lattice easily, making it ideal for writing.
In the above picture, "b" shows sheets of graphene, which when stacked on top of each other makes graphite The diagram entry of "h" shows a carbon nanotube, which is a sheet of graphene rolled into a tube.
Two researchers named Andre Geim and Konstantin Novoselov discovered graphene, a single sheet of graphite (and subsequently received the Nobel Prize in Physics 2010 for it). This single atom thick sheet can have an enormous amount of applications as we continue to shrink the size of our electronic devices. In graphene, electrons have a very high mobility, and they can move very fast, making it ideal for high speed circuitry. Also, a single layer of carbon is relatively easy to see through, opening up new possibilities for digital display screen technologies.
Here's a link detailing the two researchers Nobel Prize:
http://nobelprize.org/nobel_prizes/physics/laureates/2010/#
Today's topic is on graphene and it's crystal lattice. Semiconductors are "grown" in these lattices using expensive equipment.
Carbon, in particular, grows in many different forms, from diamonds to pencil lead (yes, you can even make diamonds in a lab). Graphite is used in pencil lead because its layers detaches from the lattice easily, making it ideal for writing.
In the above picture, "b" shows sheets of graphene, which when stacked on top of each other makes graphite The diagram entry of "h" shows a carbon nanotube, which is a sheet of graphene rolled into a tube.
Two researchers named Andre Geim and Konstantin Novoselov discovered graphene, a single sheet of graphite (and subsequently received the Nobel Prize in Physics 2010 for it). This single atom thick sheet can have an enormous amount of applications as we continue to shrink the size of our electronic devices. In graphene, electrons have a very high mobility, and they can move very fast, making it ideal for high speed circuitry. Also, a single layer of carbon is relatively easy to see through, opening up new possibilities for digital display screen technologies.
Here's a link detailing the two researchers Nobel Prize:
http://nobelprize.org/nobel_prizes/physics/laureates/2010/#
Sunday, October 10, 2010
Semiconductors
Hey guys,
I'll try to start off light, as I've been at work all day and I'm beat.
The topic today is a definition of "Semiconductors." Materials that conduct electricity well are called "Conductors." Materials that are terrible at conducting electricity are called "Insulators." What if the device we're making needs something in between? What if we need to vary the conductivity of the material for many different applications? Those are "Semiconductors."
Glass is a good insulator, and copper is a great conductor. If I take something in between, such as Gallium Arsenide (GaAs), it works well for many applications other than just conducting electrity from place to place or stopping it. It's neither a conductor or an insulator. It's a semiconductor.
What if we wanted to make these Gallium Arsenide semiconductors with a wide, predictable range of conductivity for use by many other people for many different applications? We can, by "doping" the semiconductor with atoms from other elements. More on that later.
I'll try to start off light, as I've been at work all day and I'm beat.
The topic today is a definition of "Semiconductors." Materials that conduct electricity well are called "Conductors." Materials that are terrible at conducting electricity are called "Insulators." What if the device we're making needs something in between? What if we need to vary the conductivity of the material for many different applications? Those are "Semiconductors."
Glass is a good insulator, and copper is a great conductor. If I take something in between, such as Gallium Arsenide (GaAs), it works well for many applications other than just conducting electrity from place to place or stopping it. It's neither a conductor or an insulator. It's a semiconductor.
What if we wanted to make these Gallium Arsenide semiconductors with a wide, predictable range of conductivity for use by many other people for many different applications? We can, by "doping" the semiconductor with atoms from other elements. More on that later.
Subscribe to:
Posts (Atom)